Censored data paired t-test

Performs a parametric test of whether the mean difference between two columns of paired censored data equals 0. Assumes that the paired differences follow a gaussian (normal) distribution.

cen_paired(xd, xc, yd, yc, alternative = "two.sided", printstat = TRUE)

Arguments

xd	The first column of data values plus detection limits
xc	The column of censoring indicators, where 1 (or TRUE) indicates a detection limit in the xd column, and 0 (or FALSE) indicates a detected value in xd.
yd	The second column of data values plus detection limits, or a single number representing a standard / guideline value.
yc	The column of censoring indicators for yd, where 1 (or TRUE) indicates a detection limit in the yd column, and 0 (or FALSE) indicates a detected value in yd. Not needed if yd is a single standard number.
alternative	The usual notation for the alternate hypothesis. Default is “two.sided”. Options are “greater” or “less”.
printstat	Logical TRUE/FALSE option of whether to print the resulting statistics in the console window, or not. Default is TRUE.

Value

A list of statistics containing the following components:

• n Number of observations

• Z The value of the test statistic

• p.value the p-value of the test

• Mean difference the mean difference between xd and yd

Details

You may also test for whether the mean of the xd data exceeds a standard by entering the single number for the standard as yd. In that case no yc is required.

References

Helsel, D.R., 2011. Statistics for Censored Environmental Data using Minitab and R, 2nd ed. John Wiley & Sons, USA, N.J.

See also

survival::survreg

Examples

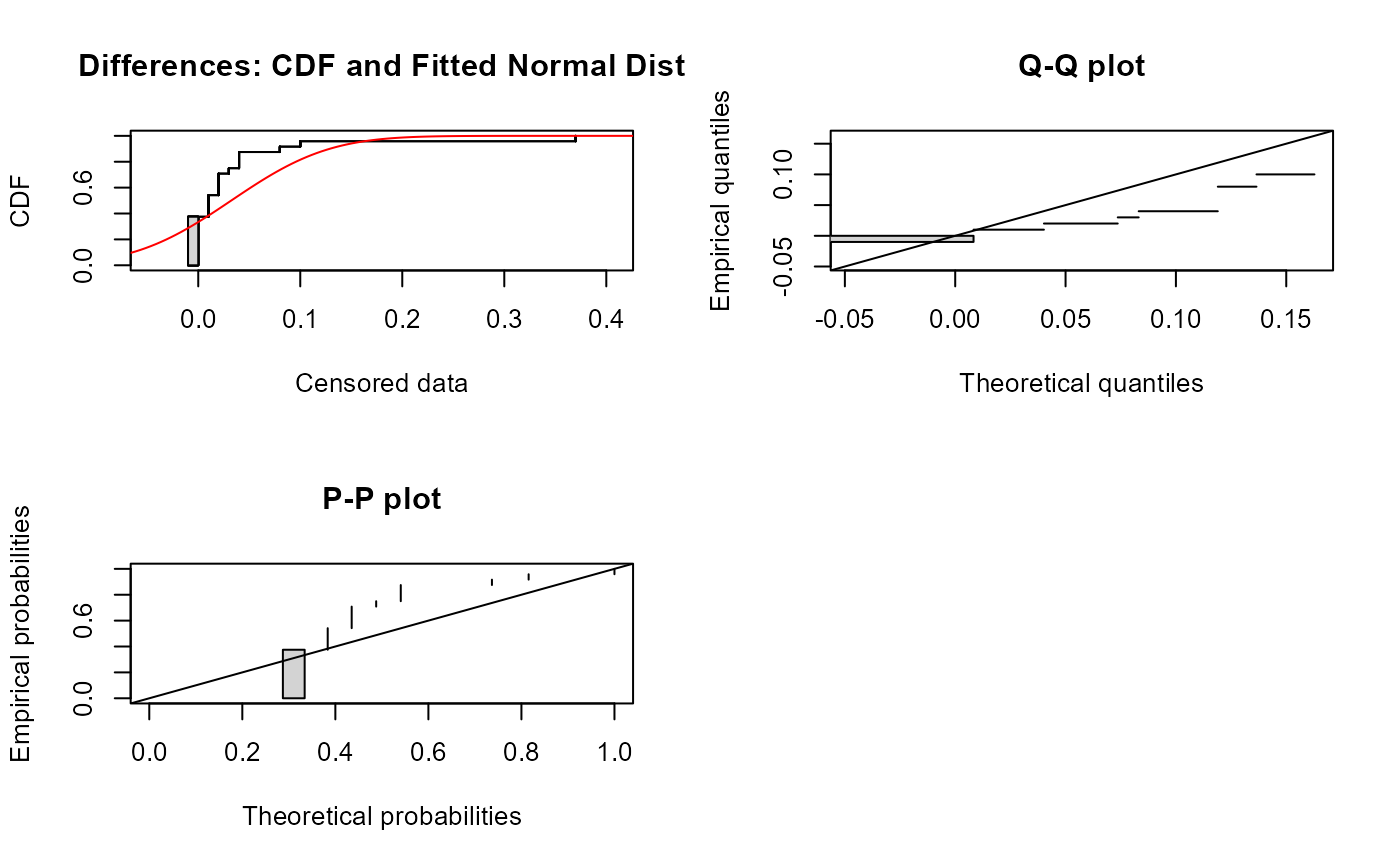
data(atrazine)

cen_paired(atrazine$June,atrazine$JuneCen,atrazine$Sept,atrazine$SeptCen)
#> Censored paired test for mean(atrazine$June - atrazine$Sept) equals 0. 
#>  alternative hypothesis: true mean difference does not equal 0. 
#>  
#>  n = 24   Z= -1.0924   p-value = 0.2747 
#>  Mean difference = -3.927 

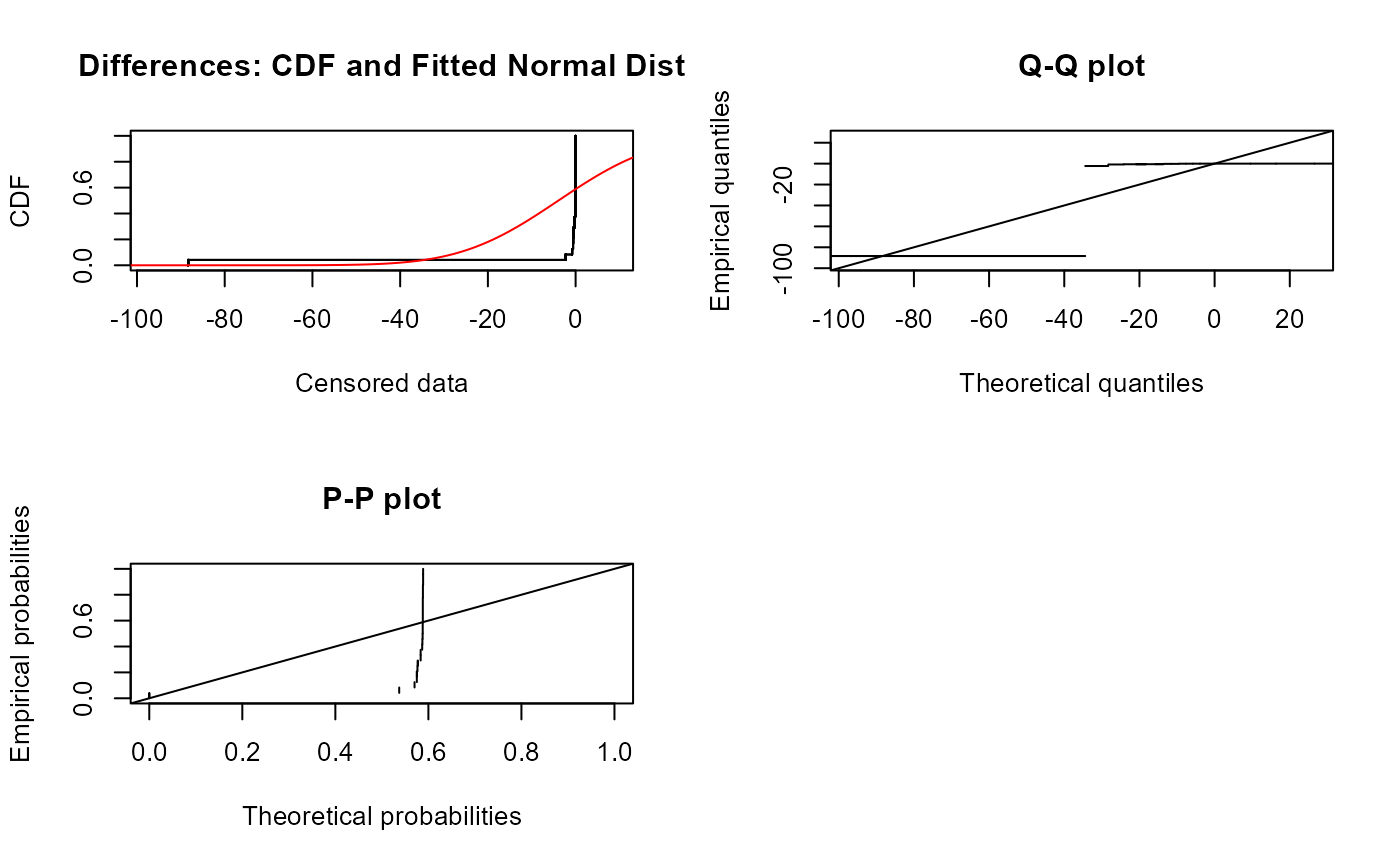# Comparing standard/guieline value
cen_paired(atrazine$June, atrazine$JuneCen, 0.01, alternative = "greater")
#>  Censored paired test for mean(atrazine$June) equals 0.01 
#>  alternative hypothesis: true mean atrazine$June exceeds 0.01. 
#>  
#>  n = 24   Z= 2.1004   p-value = 0.01785 
#>  Mean atrazine$June = 0.04231